Colligative properties are important concepts in chemistry, especially when studying solutions. These properties help us to understand how solutes affect the physical properties of a solvent. In this blog, we will learn the classification, definition, formula, and applications of colligative properties in a simple and easy way for 12th-grade students. Therefore, you should remain in this post till the end.
What Are Colligative Properties?
Colligative properties are the properties of a solution that depend on the number of solute particles in the solution, not on their nature or identity. These properties change when solutes are added to a solvent, affecting physical changes such as boiling point, freezing point, vapor pressure, and osmotic pressure. We can also defined as :
Those properties of solution which depends on the amount of solutes present in the liquid solution are called colligative properties.
Classification of Colligative Properties
There are four main types of colligative properties that you need to know:
| Colligative Properties | Effect on Solution |
| Relative Lowering of Vapor Pressure | The vapor pressure of the solution is lower than the pure solvent. |
| Elevation in Boiling Point | The boiling point of the solution increases. |
| Depression in Freezing Point | The freezing point of the solution decreases. |
| Osmotic pressure | The pressure required to stop solvent flow through a semipermeable membrane. |
Definition of Colligative Properties
Colligative properties are physical properties of solutions that change when solute particles are added to a solvent. The key factor is that the effect is determined by the number of solute particles, not by their chemical identity. For example, adding salt (NaCl) to water lowers the freezing point of water, but this effect occurs regardless of whether the salt is sodium chloride or any other solute with the same particle count.
Formula for Colligative Properties
To understand and calculate colligative properties, we use the following general formula: Property Change= K×m×i
Where:
- K is the proportionality constant (depending on the property and solvent),
- m is the molality of the solution (moles of solute per kg of solvent),
- i is the van’t Hoff factor (number of particles formed from one formula unit of solute in solution).
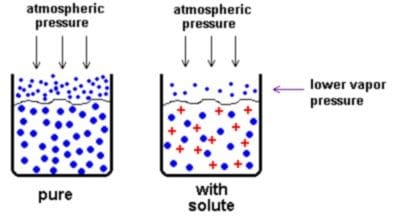
Relative Lowering of Vapor Pressure
- Definition: When a non-volatile solute is dissolved in a solvent, the vapor pressure of the solvent decreases. The decrease in vapor pressure is proportional to the number of solute particles present.
- Formula:
Relative Lowering of Vapor Pressure = (P0 – P)/(P0} = nsolute/(nsolute + nsolvent) - Where: Po is the vapor pressure of the pure solvent
- P is the vapor pressure of the solution
- nsolute is the number of moles of solute
- nsolvent is the number of moles of solvent
- Raoult’s Law: This law states that the partial vapor pressure of each volatile component of the solution is equal to the vapor pressure of the pure component multiplied by its mole fraction in the solution:

- Where: Xsolvent is the mole fraction of the solvent in the solution.
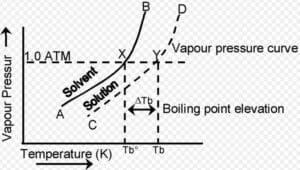
Elevation of Boiling Point
- Definition: The boiling point of a solution is always higher than that of the pure solvent. The increase in boiling point is directly proportional to the concentration of solute particles.
- Formula:

- Where:
- ΔTb is the elevation in boiling point
- Kb is the ebullioscopic constant (boiling point elevation constant) of the solvent
- m is the molality of the solute in the solution
- The boiling point elevation occurs because the solute particles reduce the number of solvent particles at the surface, thus requiring a higher temperature to reach the vapor pressure of the solvent.
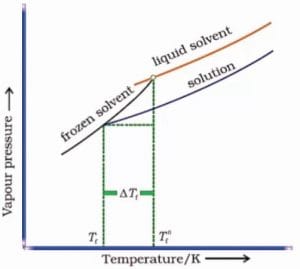
Depression of Freezing Point
Definition:
The freezing point of a solution is lower than that of the pure solvent.
Formula: ![]()
Where,
- ΔTf = Freezing point depression
- Kf = Molal freezing point depression constant
- m = Molality of the solution
Graph:
A graph depicting the decrease in freezing point as solute concentration increases.
Osmotic Pressure
Definition:
Osmotic pressure is the pressure required to stop the flow of solvent molecules through a semipermeable membrane from a pure solvent into the solution.
Formula: π=CRT
Where,
- π = Osmotic pressure
- C = Molar concentration of the solution
- R = Universal gas constant
- T = Absolute temperature
Key Points to Remember:
- Colligative properties depend only on the quantity of solute particles, not their type.
- Electrolytes dissociate in solution, producing more particles and thus have a greater effect on colligative properties compared to non-electrolytes.
- The van’t Hoff factor (i) is used to account for the effect of solute dissociation or association.
Applications of Colligative Properties:
- Antifreeze in Car Radiators: Ethylene glycol lowers the freezing point of water.
- Salting Roads in Winter: Salt lowers the freezing point of water, preventing ice formation.
- Determination of Molar Mass: Colligative properties can be used to calculate the molar mass of solutes.
Concentration of Solution: Types, Formulas, and Easy Examples for Class 12
Raoult’s Law Class 12: Definition, Derivation, Deviation and Application with Examples
Henry law Class 12: Statement, Formula, Application, Solved Examples
Conclusion
Colligative properties are fundamental concepts in physical chemistry that have practical applications in various fields. Understanding these properties helps in solving real-world problems related to solutions.
