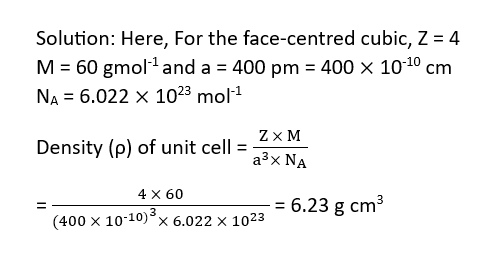Unit Cell In Solid State is important topic which helps to know the detail idea about a Crystalline solid. Here, we shall learn the definition, types of unit cell, calculation of density, number of particles in any unit cell and many more about crystal lattice. There is a need to remain in this article till end.
What is the definition of Unit Cell In Solid State?
As we know that a crystalline solid is a crystal lattice or space lattice. Its structure is either cube or cuboid which is three dimensional in space. A unit cell is the structural unit of a crystal lattice. Hence its definition can be written as:
“The smallest three dimensional portion of a complete space lattice which when repeated over and again in different directions produces the complete space lattice is called the unit cell.”
Parameters of a Unit Cell In Solid State
Those terms which decide the size and shape of the unit cell are called parameters of a unit cell. There are six parameters of a unit cell. They are followings:
- Its dimensions (lengths) along the three axis shown by thick lines and represented as a, b and c.
- Angles between the edges. They are represented as α, β, and γ.
Angle α (alpha) is between the edges b and c, β (beta) is between a and c and γ (gamma) is between a and b.
Types of Unit Cell In Solid State
The unit cell has been broadly divided into two parts. They are as:
(a) Primitive Unit Cell: The unit cells in which constituent particles are present only at the corners are called simple unit cells or primitive unit cells.
(b) Non-primitive or centred unit cell s: The unit cells in which the constituent particles are present not only at the corners but also at some other positions of the unit cells are called centred unit cells.
Further, the centred unit cells have been subdivided into three parts as following:
- Face centred unit cell (FCC): When the particles are present not only at the corners but also at the centre of each face of a unit cell, it is called face-centred unit cell.
- Body centred unit cell (BCC): When the particles are present not only at the corners but also at the centre of body of a unit cell, it is called body-centred unit cell.
- End centred unit cell (ECC): When the particles are present not only at the corners but also at the centre of any two opposite faces, it is known as end-centred unit cell.
Crystal lattice or Space lattice
In solid state, the arrangement of constituent particles in three dimensional space is called crystal lattice or space lattice. The unit cell and crystal lattice can be shown as follows:
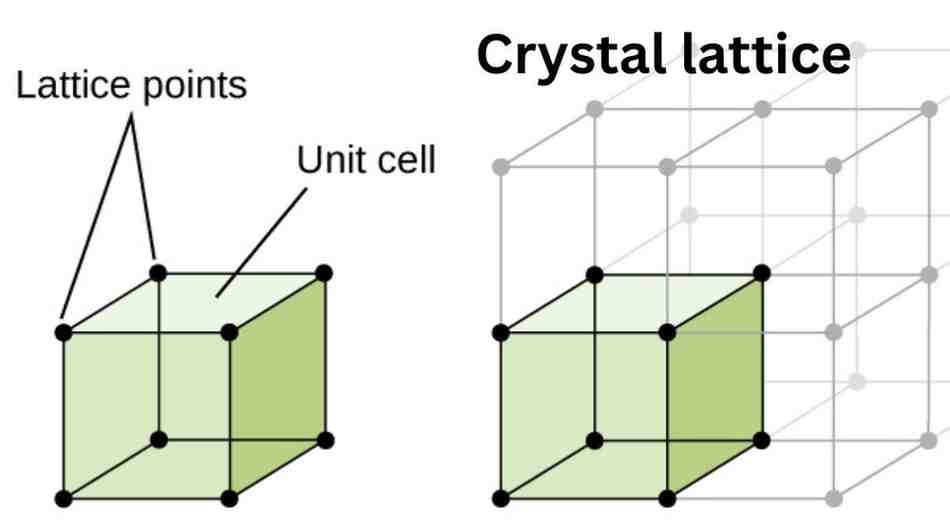
Important characteristics of crystal lattice
- Each point in a crystal lattice represents a constituent particle.
- Each point in the lattice is called lattice point or lattice site.
- The points are joined together by lines to represent the geometry of the lattice.
Crystal system or Crystal Habits
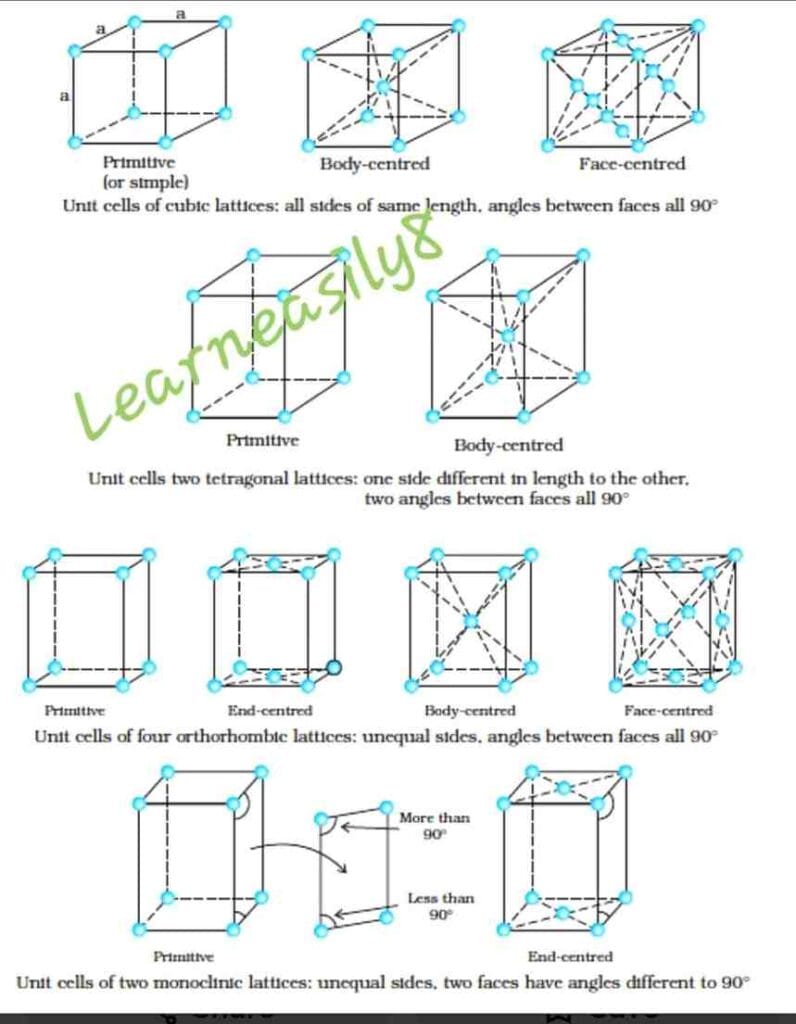
Based upon the parameters of the unit cells, there are seven types of unit cells in a crystal lattice and they are called crystal system. They are followings:
| S.No. | System | Axial Length | Axial Angles |
| 1. | Cubic | a = b = c | α = β = γ = 90o |
| 2. | Tetragonal | a = b ≠ c | α = β = γ = 90o |
| 3. | Orthorhombic or Rhombic | a ≠ b ≠ c | α = β = γ = 90o |
| 4. | Monoclinic | a ≠ b ≠ c | α = γ = 90o ≠ β |
| 5. | Triclinic | a ≠ b ≠ c | α ≠ β ≠ γ = 90o |
| 6. | Rhombohedral or Trigonal | a = b = c | α = β = γ ≠ 90o |
| 7. | Hexagonal | a = b ≠ c | α = β = 90o γ = 120o |
Bravis lattices: Based on the type of unit cells and their parameters, the crystal lattices have been further classified into 14 categories. They are known as Bravis lattices. They are shown as follows:
Determination of Particles in Unit Cell In Solid State
Based on the participation of each particle in a unit cell, there are following particles in the unit cell:
- No.of particles in simple unit cell or primitive unit cell = 8 × 1/8 = 1
- No. of particles in face centred unit cell = (8 × 1/8) + (6 × 1/2) = 4
- No. of particles in body centred unit cell = (8 × 1/8) + (1 × 1/1) = 2
- No. of particles in end centred unit cell = (8 × 1/8) + (2 × 1/2) = 2
Close Packing in Unit Cell In Solid State
The arrangement of constituent particles in three dimensional space in such a way that there is minimum empty space is called close packing.
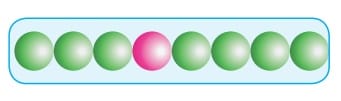
Close Packing in One Dimension:
In this arrangement, the particles which are considered as spheres are arranged in a straight line or row contacting to each other. Here, the coordination number is two.
Now we shall understand that what is coordination number in Unit Cell In Solid State?
The number of particles which are in contact of a particular particle in a crystal lattice is called the coordination number of this particle.
READ MORE: Unit Cell In Solid State: Definition Classification, Density & number of particles in unit cellSolid State Class 12 Notes: Solid State Notes in Hindi
Chemical Kinetics Class 12: Notes For Chapter 4 Chemical kinetics
Electrochemistry for 12th: Notes for chapter 3 of chemistry 12
Close Packing in Two Dimension
In this packing, the particles arranged in row are placed one above another in two ways. As a result, two types of packing are obtained in three dimension. They are followings:
(1) Square Close packing: In this packing, the row of particles are placed in such a way that the particles of each row are just above the one another. The arrangement looks as follow:
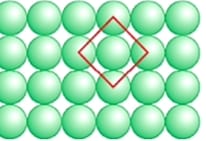
- In this arrangement, Pattern is AAAA—– types.
- The coordination number of each particle is 4.
(2) Hexagonal Close Packing:
In this packing, the rows of particles are placed one above another in such a way that the particles above rows are fit in the depression of the lower rows. The packing looks as follows:
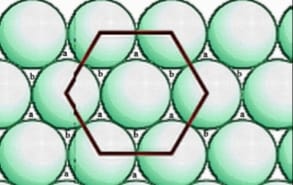
- In this arrangement, their pattern is ABABAB – – – – types.
- The coordination number of each particle is 6.
Close Packing in Three Dimension
In this packing, the layers of particles obtained in two dimension are staked one above another. In this way, two types of arrangements are possible.
(1) Close packing by square close packed layers of two dimension : In this packing, the square close packed layers are just staked one above another so that each particles are just one above another another. Their arrangement is as follows:
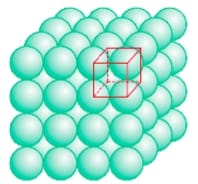
- In this arrangement, the pattern is AAAA—– types.
- The coordination number of each particle is 8.
- This lattice is known as simple cubic lattice.
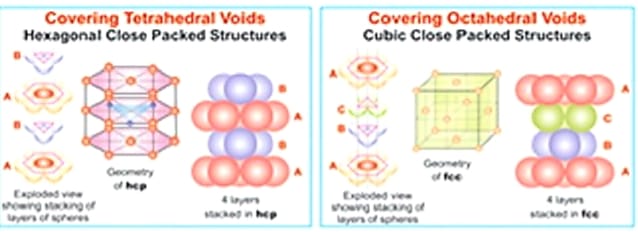
(2) Close Packing by Hexagonal close packed layers in two dimension. In this packing, when one hexagonal close packed layer is placed above another layer then two types of voids are appeared above the surface of second layer. They are tetrahedral voids and octahedral voids. Further on covering the types of voids by the particles or spheres of third layers, two types of lattices are obtained and they are followings:
(a) Hexagonal Close Packed Lattice (HCP): In this packing, tetrahedral voids are covered by the particles of third layers. The Pattern is ABAB—– types and coordination number is 12.
(b) Cubic Close Packed Lattice (CCP) In this packing, only In this packing, octahedral voids are covered by the particles of third layers. The Pattern is ABCABCABC—– types and coordination number is 12.
Packing Fraction in Unit Cell In Solid State
The part by volume of constituent particles or spheres occupy per unit volume of a unit cell is called packing fraction. That means Packing Fraction = Total volume of particles/ Volume of unit cell.
Now, we shall know about the determination of packing fraction in every types of unit cell one by one in the following ways:-
packing fraction in primitive unit cell or simple unit cell.
In primitive unit cell, the constituent particles are present only at the corners hence, a = 2r
where a = edge length in unit cell and r is the radius of particles. 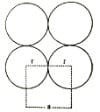
Now, the volume of the unit cell = (a)3 = (2r)3 = 8r3 and volume of each particle = 4 /3. π r3 ,
and No. Of particles in simple unit cell = 1, hence total volume in this unit cell = 4 /3. π r3 .
Now packing fraction in simple unit cell = (4 /3. π r3) / 8r3 = 0.524 and percentage occupied = 52.4%
packing fraction in face centred unit cell
Let the edge length of a face centered unit cell be “a” and radius of the particles be “r”.
Again in face centered unit cell, 4r = √2a or a = 4r/√2 and Volume of a unit cell = (a)3
∴ volume of the unit cell = (4r/√2)3 = 32r3/√2
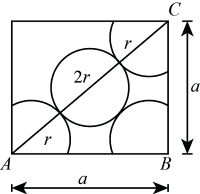
The Volume of a particle or sphere = 4πr3/3 and no of particles in each FCC unit cell = 4
∴ volume of total particles in this unit cell = 4 × 4πr3/3 = 16πr3/3
Hence, packing fraction in face centered unit cell = (16πr3/3)/32r3/√2 = π√2/6 = 0.74
and % occupied = 74%
packing fraction in body centred unit cell
Let the edge length of a body centered unit cell be “a” and radius of the particles be “r”.
Again in body centered unit cell, 4r = √3a or a = 4r/√3 and Volume of a unit cell = (a)3
∴ volume of the unit cell = (4r/√3)3 = 64r3/3√3
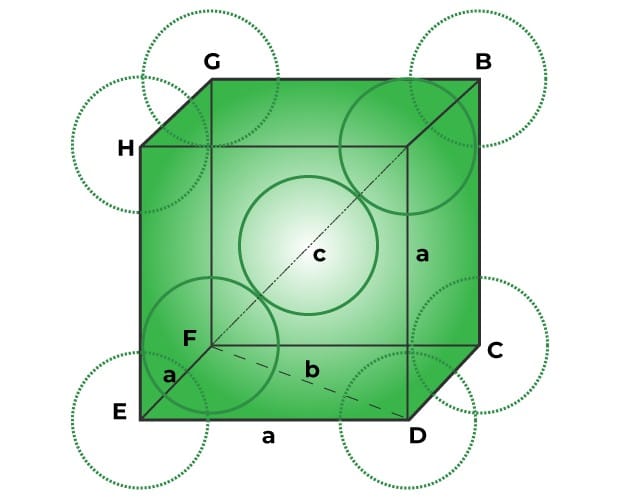
The Volume of a particle or sphere = 4πr3/3 and no of particles in each BCC unit cell = 2
∴ volume of total particles in this unit cell = 2× 4πr3/3 = 8πr3/3
Hence, packing fraction in body centered unit cell = (8πr3/3)/64r3/3√3 = π√3/8 = 0.68 and % occupied = 68%
Voids in the Unit Cell In Solid State
The vacant space left behind during close packing inside the unit cell is called Void. In the three-dimensional close packing from hexagonal close packed layers, there are two types of voids.
- Tetrahedral voids
- Octahedral voids
Tetrahedral Voids: Those voids which are surrounded by four particles or spheres in a crystal lattice are called Tetrahedral Voids.

Octahedral Voids: Those voids which are surrounded by six particles or spheres in a crystal lattice are called Octahedral Voids.
Relation Between Radius of Voids and Spheres or Particles
- Radius (r) of the tetrahedral void = 0.225 R (radius of sphere)
- Radius (r) of the octahedral void = 0.414 R (radius of sphere)


A sphere fitting into the octahedral void is shown in the figure. A sphere below and a sphere above this central sphere have not been shown in the figure. Obviously, ABC is a right triangle. Applying Pythagoras theorem.

Relation between no. Of Particles and Voids
(1) No. of particles = No. Of Octahedral voids = N
(2) No. Of the octahedral voids = 2 × No. of the tetrahedral voids. Let us consider it by the following example.
Example : In an Ionic compound, the anions (N) form cubic close type of packing while the cations (M) occupy one third of the tetrahedral voids. Deduce the empirical formula of the compound and the coordination number of (M) ions.
Solution : suppose no. of anions = n
tetrahedral voids = 2n ∴ no of cations = 2n/3 Now, Ratio of cations : anions = 2n/3 : n = 2n : 3n = 2 : 3
Hence , the formula will be M3N2. As each tetrahedral voids are surrounded by 4 ions. Hence, coordination number of M ion = 4.
Calculation of Density of a Cubic Crystal from its Edges
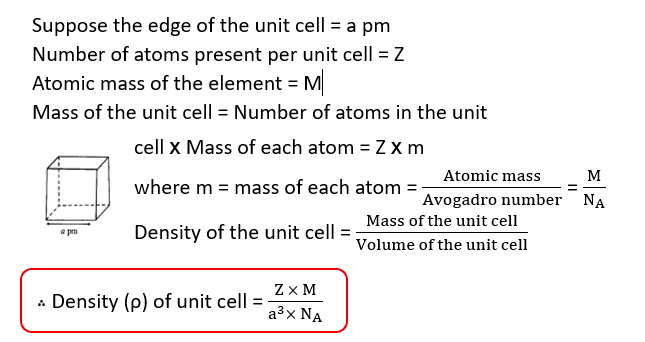
Example: A face centered cubic element (atomic mass 60) has a cell- edge of 400 pm. What is its density?